 Világbajnok Inverz Laplace Transzformáció
Világbajnok Inverz Laplace Transzformáció
Az MTA-BME Információs Rendszerek Modellezése kutatócsoport és a BME VIK Hálózati Rendszerek és Szolgáltatások Tanszék kutatói a villamosmérnöki és informatikai tudományokban alapvető fontosságú Laplace transzformációval kapcsolatban értek el átütő eredményt. A kutatócsapat (Horváth Gábor, Horváth Illés, Telek Miklós) olyan új, numerikus inverz Laplace transzformációs eljárást dolgozott ki, amely két alapvető problémát old meg egyszerre, a Gibbs oszcillációt (“túllövés”, “alullövés”) és a numerikus stabilitást. Az új eljárás (CME, Concentrated Matrix Exponential) esélyes a “világbajnoki címre”, mivel minden eddig ismert módszernél pontosabb eredményt produkál. Az eredményekről a szerzők tanulmánya a rangos Performance Evaluation folyóiratban jelent meg.
A numerikus eljárás egy, a csapat által művelt szélesebb kutatási terület, a tömegkiszolgálási rendszerekben hatékonyan alkalmazható mátrix-exponenciális eloszlás vizsgálatának eredménye. Az új módszer központi eleme a Dirac-delta függvény olyan, mátrix-exponenciális sűrűségfüggvénnyel való közelítése, amely a nem-negatív értékkészlete miatt biztosítja az oszcilláció-mentességet. Az “aritmetikai zaj” hatása is nagyságrendekkel kisebb az új eljárásban. Ez azt is jelenti, hogy adott számábrázolási rendszerben az eddig ismert módszerekhez képest nagyságrenddel több ponton (tehát nagyobb pontossággal) lehet kiértékelni az inverz transzformációt.
Gondoljunk csak bele, hogyan értékeljük az eddig ismert módszerek alkalmazásával kapott eredményeket abban az esetben, ha valamiféle csillapodó periodikus viselkedést tapasztalunk, vagy zajszerű jellel modulált függvények jelennek meg? Az ilyen hibás inverz transzformáción alapuló következtetések rendkívül félrevezetőek lehetnek, hiszen ezeket a jelenségeket a nemkívánatos Gibbs oszcilláció és az aritmetikai zaj is okozhatja. A CME módszer alkalmazásával ez nem fordulhat elő!
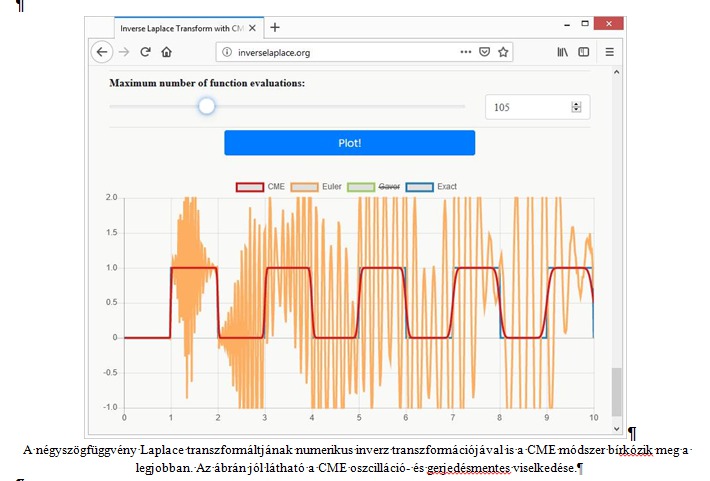
Az új módszerről rövid angol nyelvű ismertető és demó is található az alábbi linkeken:
http://inverselaplace.org/#demo
http://www.maths.utas.edu.au/People/oreilly/mam/slides_MAM10/talk_illes_horvath.pdf
A cikk az alábbi linkről tölthető le:
https://www.sciencedirect.com/science/article/pii/S0166531619302457

